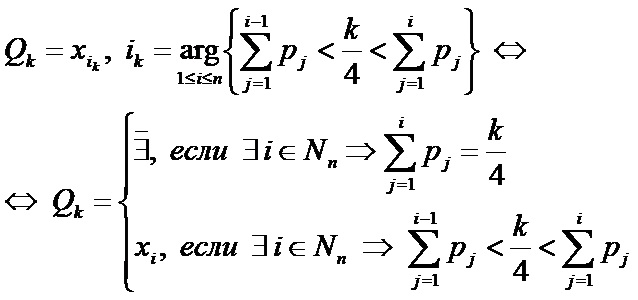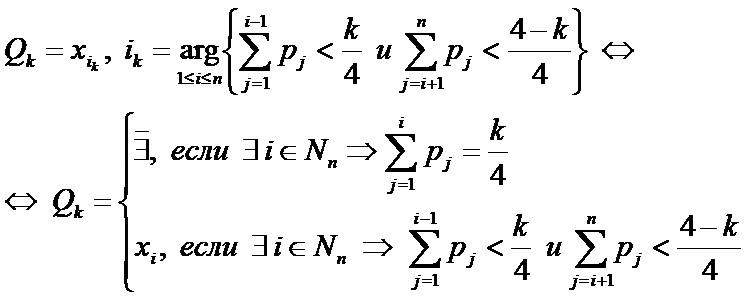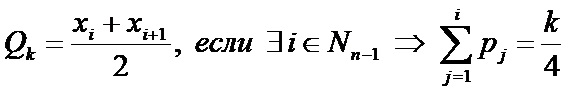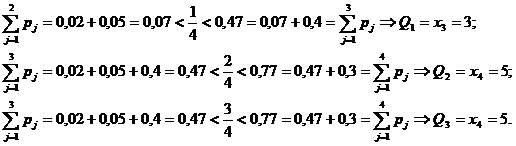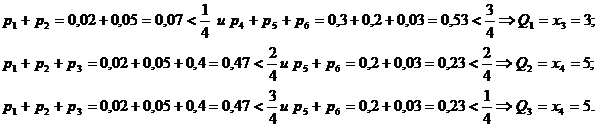Квартиль дискретной случайной величины — различия между версиями
(начало) |
|||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 9: | Строка 9: | ||
'''Q<sub>i</sub>''' — [[Квартиль непрерывной случайной величины|квартиль]], характеризующая '''i''' четвертей совокупности, — это граница между '''i'''-ой и '''i+1'''-ой частями, '''1≤i<4'''. | '''Q<sub>i</sub>''' — [[Квартиль непрерывной случайной величины|квартиль]], характеризующая '''i''' четвертей совокупности, — это граница между '''i'''-ой и '''i+1'''-ой частями, '''1≤i<4'''. | ||
== Формулы: == | == Формулы: == | ||
| + | [[файл:КВА20.JPG]] | ||
| + | |||
[[файл:КВА21.JPG]] | [[файл:КВА21.JPG]] | ||
*У дискретной случайной величины может не быть '''k'''-ой квартили, '''1≤k<4'''. | *У дискретной случайной величины может не быть '''k'''-ой квартили, '''1≤k<4'''. | ||
| Строка 16: | Строка 18: | ||
[[файл:КВА22.JPG]] | [[файл:КВА22.JPG]] | ||
*Квартиль '''Q<sub>2</sub>''' равна [[Медиана дискретной случайной величины|медиане]] '''Me'''. | *Квартиль '''Q<sub>2</sub>''' равна [[Медиана дискретной случайной величины|медиане]] '''Me'''. | ||
| + | == Пример == | ||
| + | [[файл:Прим01.png]] | ||
| + | === Решение 1 === | ||
| + | [[файл:Ква011.png]] | ||
| + | === Решение 2 === | ||
| + | [[файл:Ква012.png]] | ||
== [[Характеристики дискретной случайной величины|Другие формулы:]] == | == [[Характеристики дискретной случайной величины|Другие формулы:]] == | ||
{{Список ДСВ}} | {{Список ДСВ}} | ||
== Ссылки == | == Ссылки == | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
| − | [[Категория:Математическая статистика]] | + | [[Категория:Математика]][[Категория:Математическая статистика]] |
Текущая версия на 05:22, 10 апреля 2023
Квартиль — это числовая характеристика случайной величины, характеризующая четверти совокупности.
Содержание
Обозначения:
n — число значений дискретной случайной величины;
xj — j-ое значение случайной величины;
pj — вероятность появления j-ого значения случайной величины;
Qi — квартиль, характеризующая i четвертей совокупности, — это граница между i-ой и i+1-ой частями, 1≤i<4.
Формулы:
- У дискретной случайной величины может не быть k-ой квартили, 1≤k<4.
При отсутствии k-ой квартили у дискретной случайной величины, если в упорядоченном ряду её значений есть накопительные от начала суммы вероятностей равные k/4, иногда применяют вспомогательную формулу:
- Квартиль Q2 равна медиане Me.