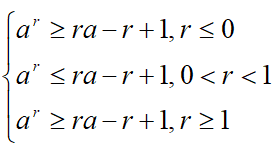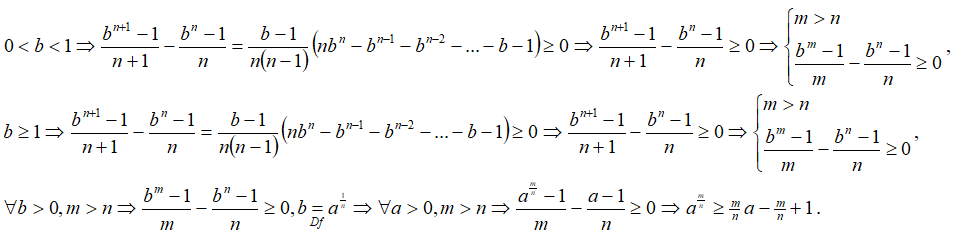Неравенство r-степени числа — различия между версиями
м |
м |
||
| Строка 2: | Строка 2: | ||
'''Неравенство ''r''-степени числа – положительное число ''a'' в действительной степени ''r'' не меньше выражения ''ra-r+1''.''' | '''Неравенство ''r''-степени числа – положительное число ''a'' в действительной степени ''r'' не меньше выражения ''ra-r+1''.''' | ||
== Обозначения == | == Обозначения == | ||
| − | '''m,n''' – натуральные числа, '''m>n'''; | + | '''m, n''' – натуральные числа, '''m>n'''; |
'''q''' – рациональное число больше 1, '''q=m/n'''; | '''q''' – рациональное число больше 1, '''q=m/n'''; | ||
| Строка 8: | Строка 8: | ||
'''r''' – действительное число; | '''r''' – действительное число; | ||
| − | '''a''' – | + | '''a, b''' – положительные действительные числа. |
== Формула неравенства == | == Формула неравенства == | ||
[[файл:НСЧ02.png]] | [[файл:НСЧ02.png]] | ||
Версия 17:23, 19 мая 2025
Неравенство r-степени числа – положительное число a в действительной степени r не меньше выражения ra-r+1.
Обозначения
m, n – натуральные числа, m>n;
q – рациональное число больше 1, q=m/n;
r – действительное число;
a, b – положительные действительные числа.
Формула неравенства
Доказательство
Другие неравенства:
- неравенство n-степени числа;
- неравенство r-степени числа;
- неравенство Йенсена;
- неравенство Юнга;
- неравенство Коши;
- неравенство средних взвешенных;
- неравенство p-ичных средних;
- обобщённое неравенство средних;
- неравенство взвешенных p-ичных средних;
- неравенство Коши-Буняковского;
- интегральное неравенство Коши-Буняковского;
- неравенство Минковского;
- обобщённое неравенство Минковского;
- интегральное неравенство Минковского;
- неравенство Гёльдера;
- обобщённое неравенство Гёльдера;
- интегральное неравенство Гёльдера;
- неравенство Фань Цзы;
- неравенство Маркова;
- неравенство Чебышёва.
Литература
- Беккенбах Э., Беллман Р. Неравенства. М.: КомКнига, под ред. В.И.Левина, Изд.2, 2007, стр.24.