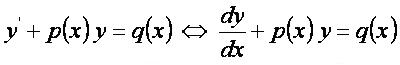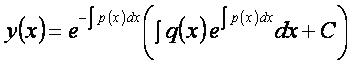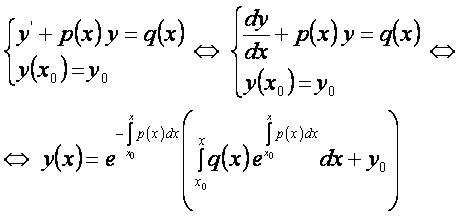Линейное дифференциальное уравнение

Линейные дифференциальные уравнения — это такие, в которых функция f(x,y) (равная производной y^’) линейная функция относительно функции y.

Будем рассматривать линейные дифференциальные уравнения вида y^’+p(x)y=q(x).

Обозначения

x – переменная - аргумент функции;

y – переменная – функция;

y^’ – производная функции;

y^’=f(x,y) – общий вид дифференциального уравнения, разрешённого относительно производной.

Дифференциальное уравнение

Общее решение

Частное решение

Другие дифференциальные уравнения:

• с разделяющимися переменными;
• однородное;
• линейное;
• уравнение Бернулли;
• уравнение в полных дифференциалах;
• уравнение Клеро;
• уравнение второго порядка, не содержащее y и y^’;
• уравнение второго порядка, не содержащее y;
• уравнение второго порядка, не содержащее x;
• однородное уравнение второго порядка с постоянными коэффициентами;
• неоднородное уравнение второго порядка с постоянными коэффициентами;
• уравнение n-ого порядка, содержащее только переменную x;
• однородное уравнение n-ого порядка с постоянными коэффициентами;
• неоднородное уравнение n-ого порядка с постоянными коэффициентами;
• общее дифференциальное уравнение.

Ссылки

• Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973, стр.536.