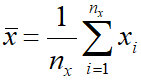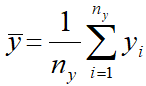Гипотеза о равенстве дисперсий — различия между версиями
м |
м |
||
| Строка 16: | Строка 16: | ||
[[файл:СРЕД06.png]]<!--<math>\bar x_\text{В} = \bar x</math>--> — средняя в выборке X, [[файл:СРЕД07.png]]<!--<math> \bar x = \frac{1}{n_x} \sum\limits_{i=1}^{n_x}{x_i}</math>-->; | [[файл:СРЕД06.png]]<!--<math>\bar x_\text{В} = \bar x</math>--> — средняя в выборке X, [[файл:СРЕД07.png]]<!--<math> \bar x = \frac{1}{n_x} \sum\limits_{i=1}^{n_x}{x_i}</math>-->; | ||
| − | [[файл:СРЕД16.png]]<!--<math>\bar y_\text{В} = \bar y</math>--> — средняя в выборке Y, [[файл: | + | [[файл:СРЕД16.png]]<!--<math>\bar y_\text{В} = \bar y</math>--> — средняя в выборке Y, [[файл:СРЕД17.png]]<!--<math> \bar y = \frac{1}{n_y} \sum\limits_{i=1}^{n_y}{y_i}</math>-->; |
| − | '''<big>s<sub>x</sub></big>''' — исправленное среднеквадратическое отклонение в выборке X, [[файл: | + | '''<big>s<sub>x</sub></big>''' — исправленное среднеквадратическое отклонение в выборке X, [[файл:СРЕД08.png]]<!--<math> s_x = \sqrt{\frac{1}{n_x -1}\sum\limits_{i=1}^{n_x}(x_i- \bar x)^2}</math>-->; |
'''<big>s<sub>y</sub></big>''' — исправленное среднеквадратическое отклонение в выборке Y, [[файл:СРЕД18.png]]<!--<math> s_y = \sqrt{\frac{1}{n_y -1}\sum\limits_{i=1}^{n_y}(y_i- \bar y)^2}</math>-->; | '''<big>s<sub>y</sub></big>''' — исправленное среднеквадратическое отклонение в выборке Y, [[файл:СРЕД18.png]]<!--<math> s_y = \sqrt{\frac{1}{n_y -1}\sum\limits_{i=1}^{n_y}(y_i- \bar y)^2}</math>-->; | ||
Версия 09:22, 20 февраля 2025
Гипотеза о равенстве дисперсий — гипотеза о том, что дисперсии двух совокупностей равны.
Обозначения
nx — число значений в выборке X;
ny — число значений в выборке Y;
— средняя генеральной совокупности X;
— средняя генеральной совокупности Y;
DxГ — дисперсия генеральной совокупности X;
DyГ — дисперсия генеральной совокупности Y;
— средняя в выборке X, 
;
— средняя в выборке Y, 
;
sx — исправленное среднеквадратическое отклонение в выборке X,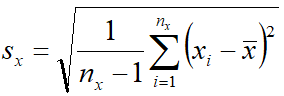 
;
sy — исправленное среднеквадратическое отклонение в выборке Y,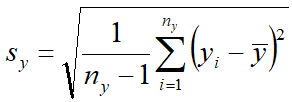 
;
α — уровень значимости — вероятность ошибки 1-го рода;
γ=1-α — коэффициент доверия;
F — переменная распределения Фишера-Снедекора;
kx — число степеней свободы в выборке X, kx=nx-1;
ky — число степеней свободы в выборке Y, ky=ny-1;
FF(F,kx,ky) — интегральная функция распределения Фишера-Снедекора.
Fтабл(αтабл,kx,ky)=FF-1(1-αтабл,kx,ky) — выражение Fтабл через интегральную функцию Фишера-Снедекора;
αтабл(Fтабл,kx,ky)=P(F>F1-αтабл,kx,ky) — соответствие веороятности для табличного значения Fтабл.
Гипотезы о дисперсиях
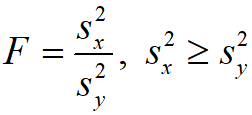— статистика, имеющая распределение Фишера-Снедекора.
Пример 1
H0:DxГ=DyГ;
H1:DxГ>DyГ;
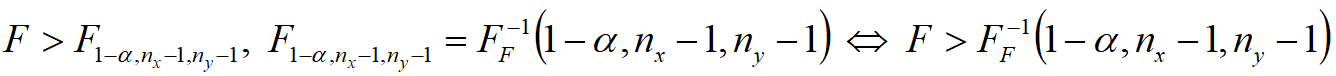— критерий отклонения гипотезы H0.
Другие гипотезы:
- Гипотеза о средней равной числу при известной дисперсии;
- Гипотеза о средней равной числу при неизвестной дисперсии;
- Гипотеза о дисперсии равной числу при известной средней;
- Гипотеза о дисперсии равной числу при неизвестной средней;
- Гипотеза о равенстве дисперсий;
- Гипотеза о равенстве межгрупповой и внутригрупповой дисперсий;
- Гипотеза о равенстве нескольких дисперсий;
- Гипотеза о равенстве средних при известных дисперсиях;
- Гипотеза о равенстве разности средних числу при известных дисперсиях;
- Гипотеза о равенстве средних при неизвестных равных дисперсиях;
- Гипотеза о равенстве средних при неизвестных дисперсиях;
- Гипотеза о вероятности равной числу;
- Гипотеза о равенстве вероятностей;
- Гипотеза о нормальном законе распределения;
- Гипотеза об отсутствии линейной корреляционной связи;
- Гипотеза о коэффициенте линейного уравнения регрессии равном нулю;
- Гипотеза о коэффициенте линейного уравнения множественной регрессии равном нулю;
- Гипотеза о значимости линейного уравнения регрессии;
- Гипотеза о значимости линейного уравнения множественной регрессии;
- Гипотеза о коэффициенте корреляции равном числу;
- Гипотеза о коэффициенте корреляции равном нулю;
- Гипотеза о равенстве коэффициентов корреляции.
