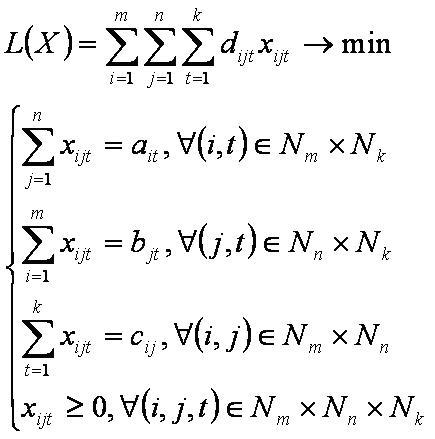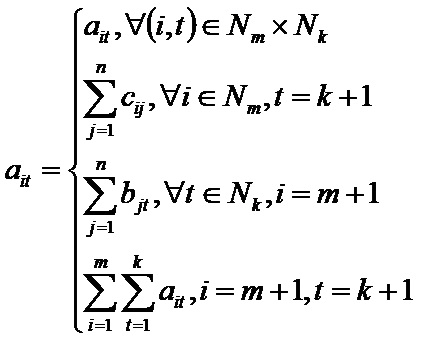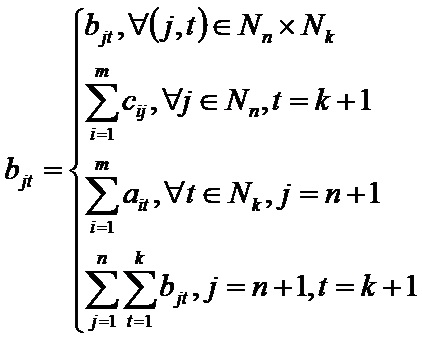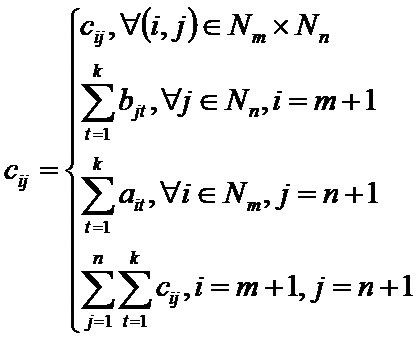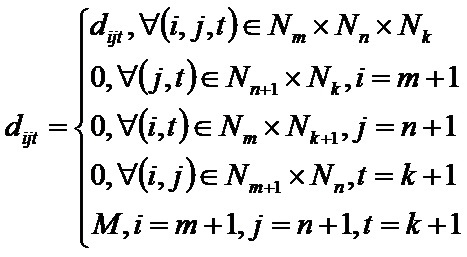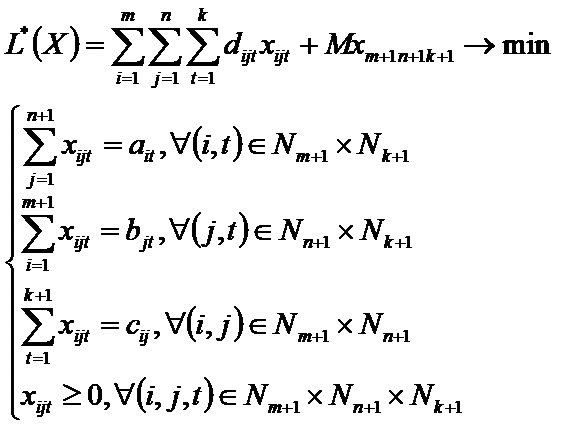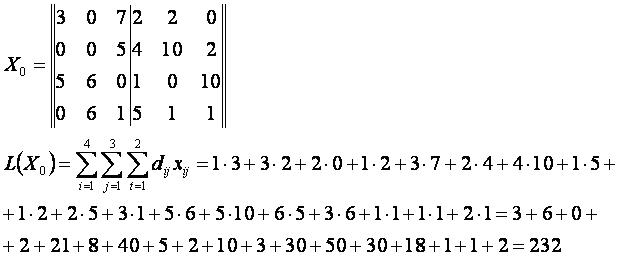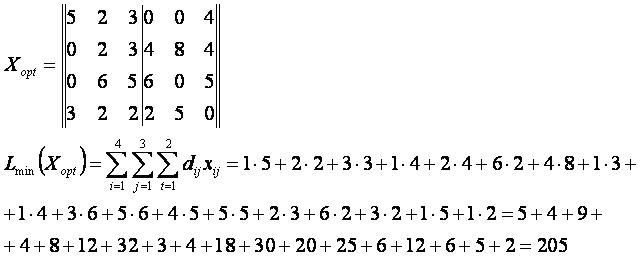Трёхиндексная транспортная задача — различия между версиями
м |
м |
||
| (не показано 15 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | [[файл:ТТЗ. | + | [[файл:ТТЗ.JPG|thumb|300|[[Математическая модель]] ТТЗ]] |
'''Трёхиндексная транспортная задача (ТТЗ)''' – это многопродуктовая [[транспортная задача]] оптимизации перевозок, являющаяся трёхмерным обобщением транспортной задачи. | '''Трёхиндексная транспортная задача (ТТЗ)''' – это многопродуктовая [[транспортная задача]] оптимизации перевозок, являющаяся трёхмерным обобщением транспортной задачи. | ||
== Постановка задачи ТТЗ == | == Постановка задачи ТТЗ == | ||
Пусть имеется '''m''' поставщиков '''(A1,A2,…,Am)''', '''n''' потребителей '''(B1,B2,…,Bn)''' и '''k''' различных продуктов '''(C1,C2,…,Ck)'''. Пусть заданы объёмы поставок '''a<sub>it</sub>''' продукта '''Ct''' поставщиком '''Ai''', объёмы потребностей '''b<sub>jt</sub>''' в продукте '''Ct''' у потребителя '''Bj''', объёмы перевозок '''c<sub>ij</sub>''' от поставщика '''Ai''' к потребителю '''Bj'''. Пусть известны транспортные расходы '''d<sub>ijt</sub>''' на перевозку единицы продукта '''Ct''' от поставщика '''Ai''' к потребителю '''Bj''' и необходимо определить план перевозок с минимальной суммой транспортных расходов, тогда трёхиндексная [[Транспортная задача с промежуточными пунктами|транспортная задача]] (ТТЗ) формулируется следующим образом: | Пусть имеется '''m''' поставщиков '''(A1,A2,…,Am)''', '''n''' потребителей '''(B1,B2,…,Bn)''' и '''k''' различных продуктов '''(C1,C2,…,Ck)'''. Пусть заданы объёмы поставок '''a<sub>it</sub>''' продукта '''Ct''' поставщиком '''Ai''', объёмы потребностей '''b<sub>jt</sub>''' в продукте '''Ct''' у потребителя '''Bj''', объёмы перевозок '''c<sub>ij</sub>''' от поставщика '''Ai''' к потребителю '''Bj'''. Пусть известны транспортные расходы '''d<sub>ijt</sub>''' на перевозку единицы продукта '''Ct''' от поставщика '''Ai''' к потребителю '''Bj''' и необходимо определить план перевозок с минимальной суммой транспортных расходов, тогда трёхиндексная [[Транспортная задача с промежуточными пунктами|транспортная задача]] (ТТЗ) формулируется следующим образом: | ||
| − | [[файл:ТТЗ. | + | [[файл:ТТЗ.JPG]], |
где '''x<sub>ijt</sub>''' - объём перевозок продукта '''Ct''' от поставщика '''Ai''' к потребителю '''Bj'''. | где '''x<sub>ijt</sub>''' - объём перевозок продукта '''Ct''' от поставщика '''Ai''' к потребителю '''Bj'''. | ||
| Строка 12: | Строка 12: | ||
т.е. необходимо, чтобы объём поставок каждого продукта равнялся объёму потребностей в нём, чтобы объём поставок каждого поставщика равнялся объёму перевозок от него, чтобы объём потребностей каждого потребителя равнялся объёму перевозок к нему. | т.е. необходимо, чтобы объём поставок каждого продукта равнялся объёму потребностей в нём, чтобы объём поставок каждого поставщика равнялся объёму перевозок от него, чтобы объём потребностей каждого потребителя равнялся объёму перевозок к нему. | ||
| + | == Постановка вспомогательной задачи == | ||
| + | Сформулируем задачу, таким образом, чтобы её оптимальное решение при '''x<sub>m+1n+1k+1</sub>=0''' совпадало с оптимальным решением исходной. | ||
| + | Для построения вспомогательной задачи введём новые обозначения: | ||
| + | |||
| + | '''M''' — это достаточно большое положительное число. | ||
| + | |||
| + | [[файл:ТТЗ21.JPG]]; | ||
| + | [[файл:ТТЗ22.JPG]]; | ||
| + | [[файл:ТТЗ23.JPG]]; | ||
| + | [[файл:ТТЗ24.JPG]]. | ||
| + | |||
| + | Математическая модель вспомогательной задачи принимает следующий вид: | ||
| + | |||
| + | [[файл:ТТЗ3.JPG]]. | ||
== Метод решения ТТЗ == | == Метод решения ТТЗ == | ||
Трёхиндексная [[транспортная задача]] решается методом потенциалов для решения транспортной задачи обобщённым на трёхмерный случай. | Трёхиндексная [[транспортная задача]] решается методом потенциалов для решения транспортной задачи обобщённым на трёхмерный случай. | ||
| Строка 33: | Строка 47: | ||
[[файл:ТТЗ01.JPG]] | [[файл:ТТЗ01.JPG]] | ||
=== Допустимое решение === | === Допустимое решение === | ||
| − | + | [[файл:ТТЗ11.JPG]] | |
| − | |||
[[файл:ТТЗ10.JPG]] | [[файл:ТТЗ10.JPG]] | ||
=== Решение методом потенциалов === | === Решение методом потенциалов === | ||
[[файл:ТТЗ12.JPG]] | [[файл:ТТЗ12.JPG]] | ||
| + | |||
[[файл:ТТЗ13.JPG]] | [[файл:ТТЗ13.JPG]] | ||
| + | |||
[[файл:ТТЗ14.JPG]] | [[файл:ТТЗ14.JPG]] | ||
| + | == [[Транспортные задачи|Задачи транспортного типа:]] == | ||
| + | {{Список ЗТТ}} | ||
== Другие задачи: == | == Другие задачи: == | ||
| − | {{Список | + | {{Список ЗМП}} |
== Ссылки == | == Ссылки == | ||
| − | *Емеличев В. А., Ковалев М. М., Кравцов М. К., Многогранники. Графы. Оптимизация. — М., 1981, стр.313 | + | *Емеличев В.А., Ковалев М.М., Кравцов М.К., Многогранники. Графы. Оптимизация. — М., 1981, стр.313 |
| − | *Кривопалов Ю. А. Метод потенциалов для решения трёхиндексной транспортной задачи. М.,ВИМИ, 1990г. деп.№Д08221. | + | *Кривопалов Ю.А. Метод потенциалов для решения трёхиндексной транспортной задачи. М.,ВИМИ, 1990г. деп.№Д08221. |
| − | *Кривопалов Ю. А. Метод потенциалов для решения трёхиндексной транспортной задачи. Сборник ХI конференции «Наука. Творчество» 2015, Самара, Т.1,стр.39. | + | *Кривопалов Ю.А. Метод потенциалов для решения трёхиндексной транспортной задачи. Сборник ХI конференции «Наука. Творчество» 2015, Самара, Т.1,стр.39. |
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
| − | [[Категория:Линейное программирование]][[Категория:Транспортная задача]][[Категория:Логистика]] | + | [[Категория:Математика]][[Категория:Линейное программирование]][[Категория:Транспортная задача]][[Категория:Логистика]] |
Текущая версия на 14:36, 16 февраля 2025
Трёхиндексная транспортная задача (ТТЗ) – это многопродуктовая транспортная задача оптимизации перевозок, являющаяся трёхмерным обобщением транспортной задачи.
Содержание
Постановка задачи ТТЗ
Пусть имеется m поставщиков (A1,A2,…,Am), n потребителей (B1,B2,…,Bn) и k различных продуктов (C1,C2,…,Ck). Пусть заданы объёмы поставок ait продукта Ct поставщиком Ai, объёмы потребностей bjt в продукте Ct у потребителя Bj, объёмы перевозок cij от поставщика Ai к потребителю Bj. Пусть известны транспортные расходы dijt на перевозку единицы продукта Ct от поставщика Ai к потребителю Bj и необходимо определить план перевозок с минимальной суммой транспортных расходов, тогда трёхиндексная транспортная задача (ТТЗ) формулируется следующим образом:
где xijt - объём перевозок продукта Ct от поставщика Ai к потребителю Bj.
Условия разрешимости
Для разрешимости задачи необходимо выполнение условий баланса:
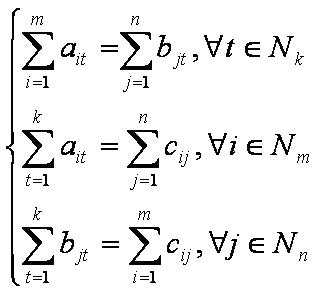
т.е. необходимо, чтобы объём поставок каждого продукта равнялся объёму потребностей в нём, чтобы объём поставок каждого поставщика равнялся объёму перевозок от него, чтобы объём потребностей каждого потребителя равнялся объёму перевозок к нему.
Постановка вспомогательной задачи
Сформулируем задачу, таким образом, чтобы её оптимальное решение при xm+1n+1k+1=0 совпадало с оптимальным решением исходной. Для построения вспомогательной задачи введём новые обозначения:
M — это достаточно большое положительное число.
Математическая модель вспомогательной задачи принимает следующий вид:
Метод решения ТТЗ
Трёхиндексная транспортная задача решается методом потенциалов для решения транспортной задачи обобщённым на трёхмерный случай. Пусть имеется допустимое опорное решение ТТЗ. Начальное допустимое опорное решение может быть получено с помощью алгоритма минимального элемента для ТТЗ. Тогда метод потенциалов для ТТЗ принимает вид.
Метод потенциалов
1.Берём допустимое опорное решение Xmxnxk и базис Zmxnxk.
2.Определяем значение целевой функции L=ΣΣΣdijtxijt и базис опорного решения Bo={(i,j,t)|zijt=1}.
3.Определяем оценку Δo и элемент (io,jo,to) с помощью алгоритма расчёта потенциалов для ТТЗ (также определяются оценки оптимальности Δijt).
4.Проверяем решение на оптимальность. Если Δo=0, то решение Xmxnxk - оптимальное и конец работы, иначе определяем E+={(i,j,t)|Δijt>=0}.
5.Определяем оценку Δx, элемент (ix,jx,tx) и новое опорное решение Xmxnxk с помощью алгоритма перераспределения перевозок для ТТЗ. Если нового допустимого опорного решения нет, то переходим к пункту 7.
6.Определяем новое значение целевой функции L=L-ΔoΔx и новый базис Bo=Bo\(ix,jx,tx)U(io,jo,to). Переходим к пункту 3.
7.Переопределяем множество E+=E+\(io,jo,to) и определяем новую оценку Δo и элемент (io,jo,to). Если новый элемент (io,jo,to) есть, то переходим к пункту 5, иначе конец работы.
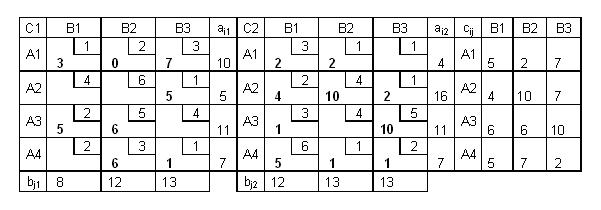
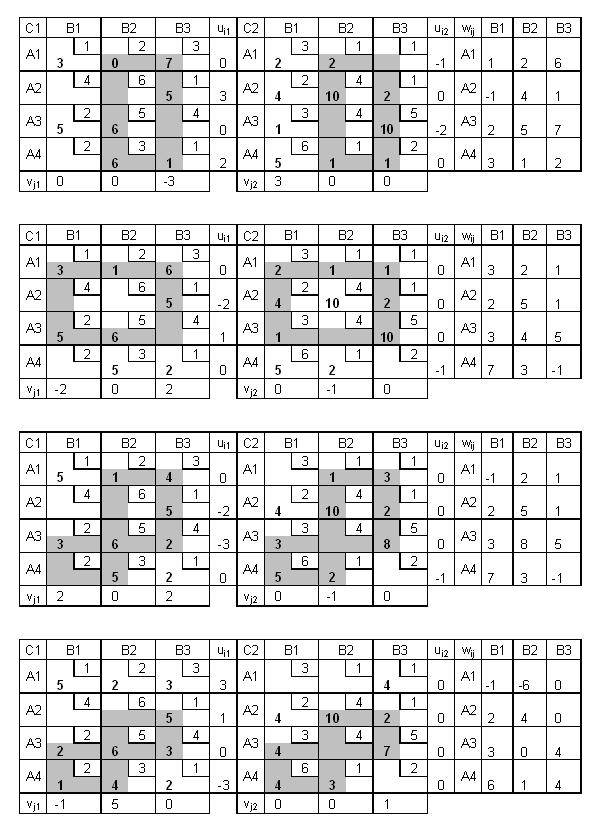
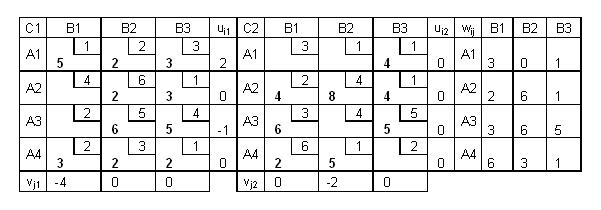
Пример ТТЗ
Допустимое решение
Решение методом потенциалов
Задачи транспортного типа:
- Транспортная задача;
- Распределительная задача;
- Задача о назначениях;
- Транспортная задача с промежуточными пунктами;
- Транспортная задача с промежуточными пунктами с запретами;
- Транспортная задача с промежуточными пунктами и ограничением по транзиту;
- Открытая транспортная задача с промежуточными пунктами;
- Открытая транспортная задача с промежуточными пунктами 1;
- Открытая транспортная задача с промежуточными пунктами 2;
- Открытая транспортная задача с промежуточными пунктами 3;
- Открытая транспортная задача с промежуточными пунктами 4;
- Трёхиндексная транспортная задача;
- Трёхиндексная транспортная задача с аксиальными суммами;
- Трёхиндексная транспортная задача с промежуточными пунктами.
Другие задачи:
Ссылки
- Емеличев В.А., Ковалев М.М., Кравцов М.К., Многогранники. Графы. Оптимизация. — М., 1981, стр.313
- Кривопалов Ю.А. Метод потенциалов для решения трёхиндексной транспортной задачи. М.,ВИМИ, 1990г. деп.№Д08221.
- Кривопалов Ю.А. Метод потенциалов для решения трёхиндексной транспортной задачи. Сборник ХI конференции «Наука. Творчество» 2015, Самара, Т.1,стр.39.
- Участник:Logic-samara