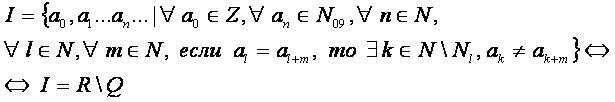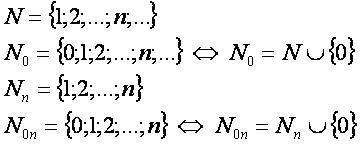Иррациональные числа

Иррациональными называются числа, которые представимы в виде бесконечной непериодической десятичной дроби.

Обозначения

N — множество натуральных чисел;

Z — множество целых чисел;

Q — множество рациональных чисел;

I — множество иррациональных чисел;

R — множество действительных (вещественных) чисел;

a₀ — целая часть числа;

a_j — цифра дробной части (мантиссы) числа, j>0;

a₀,a₁...a_n... — бесконечная непериодическая десятичная дробь.

Формулы:

,

где

Примеры:

• Число пи;
• Число Эйлера.

Дополнение

Введём обозначения:

r, r₁, r₂ — рациональные числа;

Q₁ — подмножество рациональных чисел — нижний класс сечения;

Q₂ — подмножество рациональных чисел — верхний класс сечения;

supQ₁ — верхняя граница множества Q₁;

infQ₂ — нижняя граница множества Q₂;

Q₁|Q₂ — сечение множества рациональных чисел Q.

g=supQ₁=infQ₂ — действительное число — граница сечения;

Разбиением будем считать разделение множества всех рациональных чисел на два непустых подмножества. ,

Сечением будем считать разбиение, имеющее следующие свойства: ,

Иррациональные числа можно определить как подмножество не рациональных границ множества всех сечений множества рациональных чисел.

Другие числа:

• действительные числа;
  • рациональные числа;
  • иррациональные числа;
• комплексные числа;
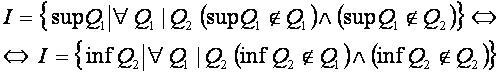
  • комплексно сопряжённые числа.

Ссылки

• Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления. Т.1, М.: Физматлит, 207, стр.20.