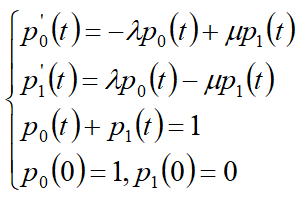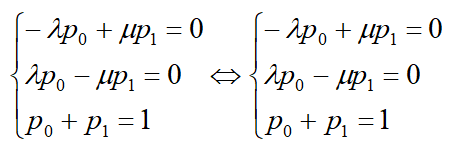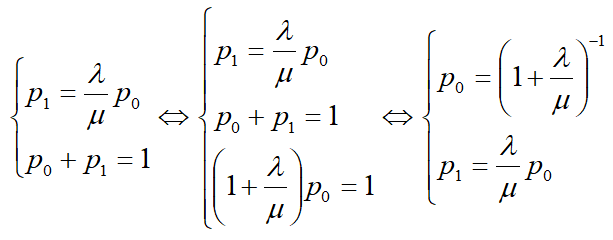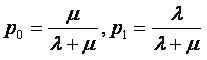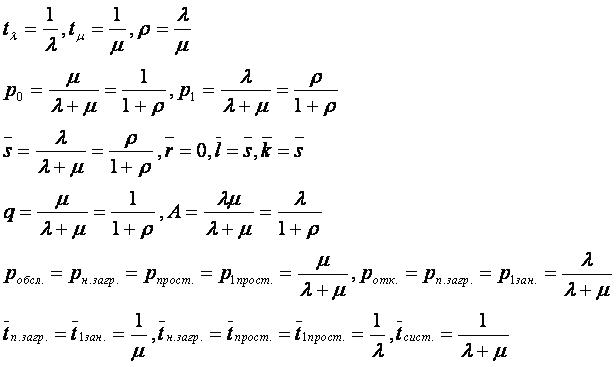Одноканальная СМО без очереди — различия между версиями
м |
|||
| (не показано 16 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | [[файл: | + | [[файл:СМО1.png|thumb|300|Одноканальная СМО без очереди]] |
| − | '''Одноканальная [[СМО | + | '''[[Одноканальная СМО с m-очередью|Одноканальная СМО]] [[СМО n-канальная без очереди|без очереди]]''' — это [[система массового обслуживания]], в которой есть один канал обслуживания, но нет очереди: если заявка приходит, в момент, когда канал свободен, то она немедленно обслуживается каналом, если заявка приходит — когда канал занят, то заявка покидает систему (теряется). |
| + | Максимальное число заявок в системе равно 1. | ||
| + | == Обозначения == | ||
| + | '''n''' – число каналов обслуживания; | ||
| + | |||
| + | '''m''' – число мест в очереди; | ||
| + | |||
| + | '''λ''' – интенсивность простейшего потока заявок; | ||
| + | |||
| + | '''μ''' – интенсивность простейшего потока обслуживания. | ||
== Описание модели == | == Описание модели == | ||
На вход одноканальной СМО поступает простейший поток заявок с интенсивностью '''λ'''. | На вход одноканальной СМО поступает простейший поток заявок с интенсивностью '''λ'''. | ||
| Строка 14: | Строка 23: | ||
Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе. | Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе. | ||
== Граф состояний == | == Граф состояний == | ||
| − | [[файл:СМО111.JPG]] | + | <!--[[файл:СМО111.JPG]]--> |
| + | '''М/М/1/0''' – Одноканальная СМО без очереди (с отказами). | ||
| + | |||
| + | [[файл:СМО1.png]] | ||
Рассмотрим множество состояний системы: | Рассмотрим множество состояний системы: | ||
| Строка 24: | Строка 36: | ||
Система дифференциальных уравнений, описывающих поведение системы, имеет вид: | Система дифференциальных уравнений, описывающих поведение системы, имеет вид: | ||
| − | [[файл:СМО121.JPG]] | + | <!--[[файл:СМО121.JPG]]--> |
| + | [[файл:СДУ1.png]] | ||
Рассмотрим стационарный режим работы системы (при '''t→∞'''). | Рассмотрим стационарный режим работы системы (при '''t→∞'''). | ||
| − | + | == Система линейных уравнений == | |
Система уравнений принимает вид: | Система уравнений принимает вид: | ||
| − | [[файл:СМО131.JPG]] | + | <!--[[файл:СМО131.JPG]]--> |
| + | [[файл:СЛУ1.png]] | ||
| + | == Решение системы линейных уравнений == | ||
| + | Решим систему относительно '''p<sub>0</sub>,p<sub>1</sub>'''. | ||
| − | + | <!--[[файл:СМО141.JPG]]--> | |
| + | [[файл:СЛУ101.png]] | ||
| − | [[файл: | + | В результате получаем решение системы:[[файл:СЛУ102.png]] |
| − | + | <!--[[файл:СМО151.JPG]]--> | |
[[файл:СМО151.JPG]] | [[файл:СМО151.JPG]] | ||
== Основные характеристики системы == | == Основные характеристики системы == | ||
| Строка 44: | Строка 61: | ||
== Ссылки == | == Ссылки == | ||
*Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969. | *Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969. | ||
| − | |||
[[Категория:Математика]][[Категория:Случайные процессы]][[Категория:Логистика]] | [[Категория:Математика]][[Категория:Случайные процессы]][[Категория:Логистика]] | ||
Текущая версия на 16:45, 28 сентября 2025
Одноканальная СМО без очереди — это система массового обслуживания, в которой есть один канал обслуживания, но нет очереди: если заявка приходит, в момент, когда канал свободен, то она немедленно обслуживается каналом, если заявка приходит — когда канал занят, то заявка покидает систему (теряется). Максимальное число заявок в системе равно 1.
Содержание
Обозначения
n – число каналов обслуживания;
m – число мест в очереди;
λ – интенсивность простейшего потока заявок;
μ – интенсивность простейшего потока обслуживания.
Описание модели
На вход одноканальной СМО поступает простейший поток заявок с интенсивностью λ.
Интенсивность простейшего потока обслуживания канала μ.
Если заявка застаёт канал свободным, она принимается на обслуживание и обслуживается каналом.
Если заявка застаёт канал занятым, то она получает отказ (покидает систему не обслуженной).
После окончания обслуживания заявки освобождается канал.
Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.
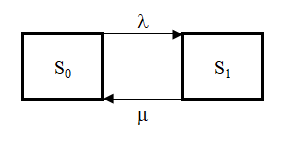
Граф состояний
М/М/1/0 – Одноканальная СМО без очереди (с отказами).
Рассмотрим множество состояний системы:
S0 – в системе нет заявки, канал свободен;
S1 – в системе имеется заявка, она обслуживается каналом.
Система дифференциальных уравнений
Система дифференциальных уравнений, описывающих поведение системы, имеет вид:
Рассмотрим стационарный режим работы системы (при t→∞).
Система линейных уравнений
Система уравнений принимает вид:
Решение системы линейных уравнений
Решим систему относительно p0,p1.
В результате получаем решение системы: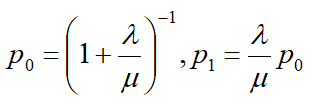
Основные характеристики системы
Другие одноканальные СМО:
- Одноканальная СМО без очереди;
- Одноканальная СМО с m-очередью;
- Одноканальная СМО с m-очередью и с ограниченным временем ожидания;
- Одноканальная СМО с бесконечной очередью;
- Одноканальная СМО с бесконечной очередью и с убывающим потоком заявок;
- Одноканальная СМО замкнутая без очереди;
- Одноканальная СМО замкнутая с m-очередью;
- Одноканальная СМО замкнутая без очереди и с k-источниками;
- Одноканальная СМО замкнутая с m-очередью и с k-источниками.
Ссылки
- Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969.
