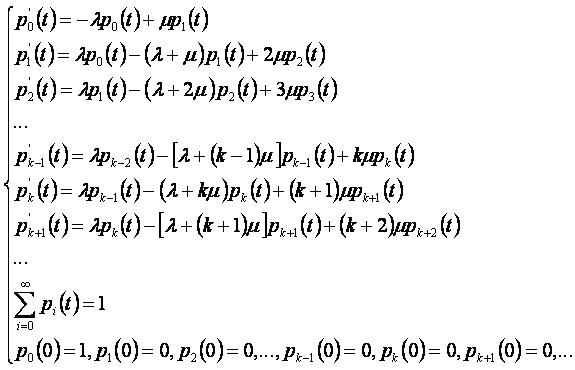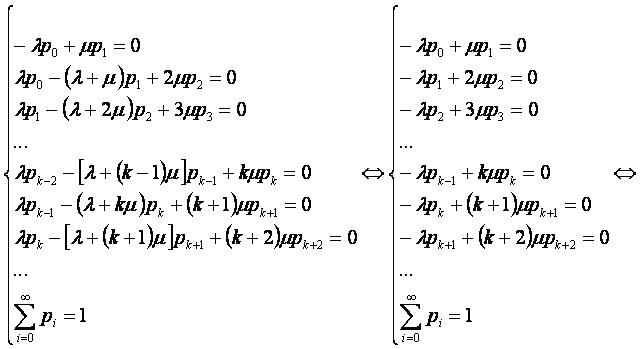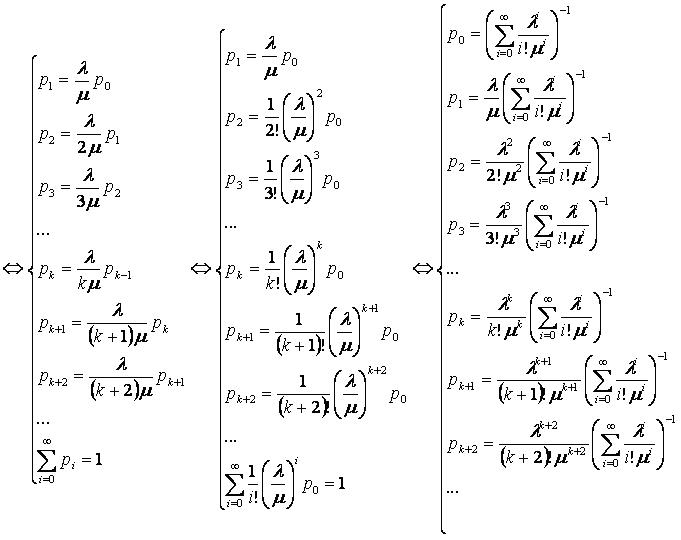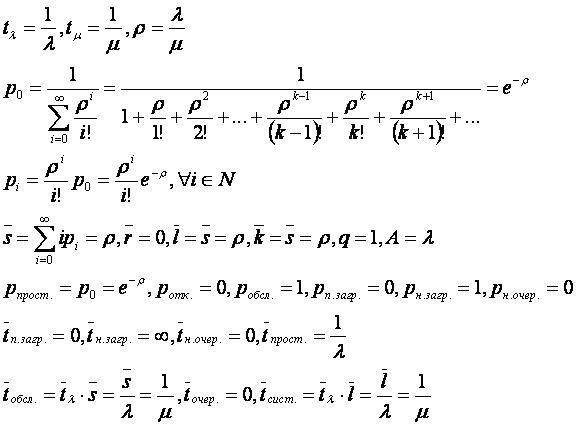СМО с бесконечным числом каналов — различия между версиями
(начало) |
м |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | [[файл: | + | [[файл:СМО8.png|thumb|300|СМО с бесконечным числом каналов]] |
'''[[СМО с бесконечной очередью|СМО с бесконечным]] числом каналов''' — это [[система массового обслуживания]], в которой любая заявка немедленно обслуживается любым одним каналом. | '''[[СМО с бесконечной очередью|СМО с бесконечным]] числом каналов''' — это [[система массового обслуживания]], в которой любая заявка немедленно обслуживается любым одним каналом. | ||
== Описание модели == | == Описание модели == | ||
| Строка 14: | Строка 14: | ||
Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе. | Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе. | ||
== Граф состояний == | == Граф состояний == | ||
| − | [[файл:СМО71.JPG]] | + | <!--[[файл:СМО71.JPG]]--> |
| + | '''М/М/∞''' – СМО с бесконечным числом каналов | ||
| + | |||
| + | [[файл:СМО8.png]] | ||
Рассмотрим множество состояний системы: | Рассмотрим множество состояний системы: | ||
| Строка 58: | Строка 61: | ||
== Ссылки == | == Ссылки == | ||
*Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969. | *Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969. | ||
| − | + | [[Категория:Математика]][[Категория:Случайные процессы]][[Категория:Логистика]] | |
| − | [[Категория:Случайные процессы]][[Категория:Логистика]] | ||
Текущая версия на 16:39, 14 августа 2025
СМО с бесконечным числом каналов — это система массового обслуживания, в которой любая заявка немедленно обслуживается любым одним каналом.
Содержание
Описание модели
На вход СМО с бесконечным числом каналов поступает простейший поток заявок с интенсивностью λ.
Интенсивность простейшего потока обслуживания каждого канала μ.
Если заявка застаёт все каналы свободными, она принимается на обслуживание и обслуживается любым одним из каналов.
Если заявка застаёт занятым хотя бы один канал, то она принимается на обслуживание любым из свободных каналов и обслуживается до конца.
После окончания обслуживания одной заявки освобождается один канал.
Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.
Граф состояний
М/М/∞ – СМО с бесконечным числом каналов
Рассмотрим множество состояний системы:
S0 – в системе нет ни одной заявки, все каналы свободны;
S1 – в системе имеется одна заявка, она обслуживается одним каналом;
S2 – в системе имеется две заявки, они обслуживается двумя каналами;
…;
Sk-1 – в системе имеется (k-1)-заявок, они обслуживаются (k-1)-каналами;
Sk – в системе имеется k-заявок, они обслуживаются k-каналами;
Sk+1 – в системе имеется (k+1)-заявок, они обслуживаются (k+1)-каналами;
….
Система дифференциальных уравнений
Система дифференциальных уравнений, описывающих поведение системы, имеет вид:
Рассмотрим стационарный режим работы системы (при t→∞).
Система уравнений принимает вид:
Суммируя в системе уравнения с первого до i-го (i=1,∞), получаем упрощённый вид системы.
Решим систему относительно p0,p1,…,pk,….
В результате получаем решение системы:
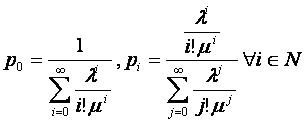
Основные характеристики системы
Другие СМО:
Ссылки
- Овчаров Л.А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969.